# 理论基础
# 二叉树的种类
# 满二叉树
如果一棵二叉树只有度为 0 的结点和度为 2 的结点,并且度为 0 的结点在同一层上,则这棵二叉树为满二叉树。
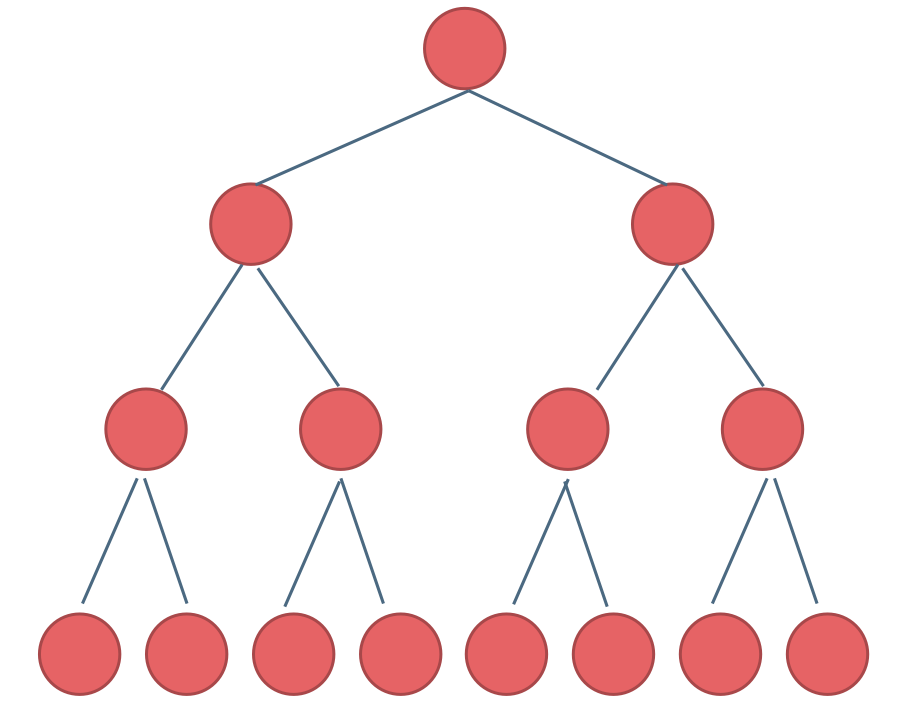
- 深度为 k
- 有 个节点
# 完全二叉树
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(h 从 1 开始),则该层包含 个节点。
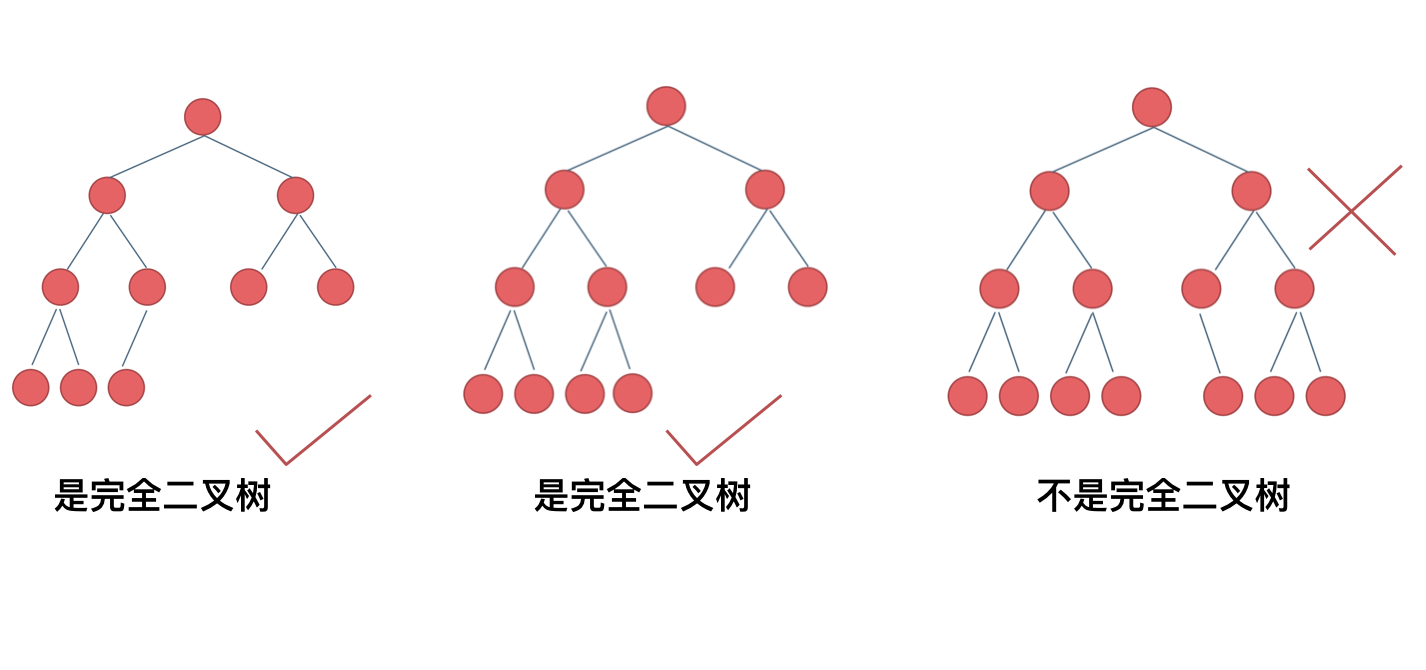
# 二叉搜索树
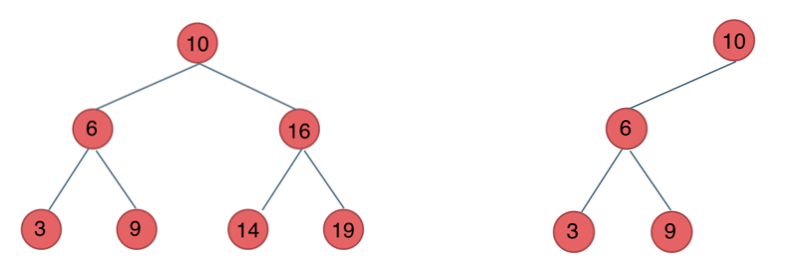
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
# 平衡二叉搜索树
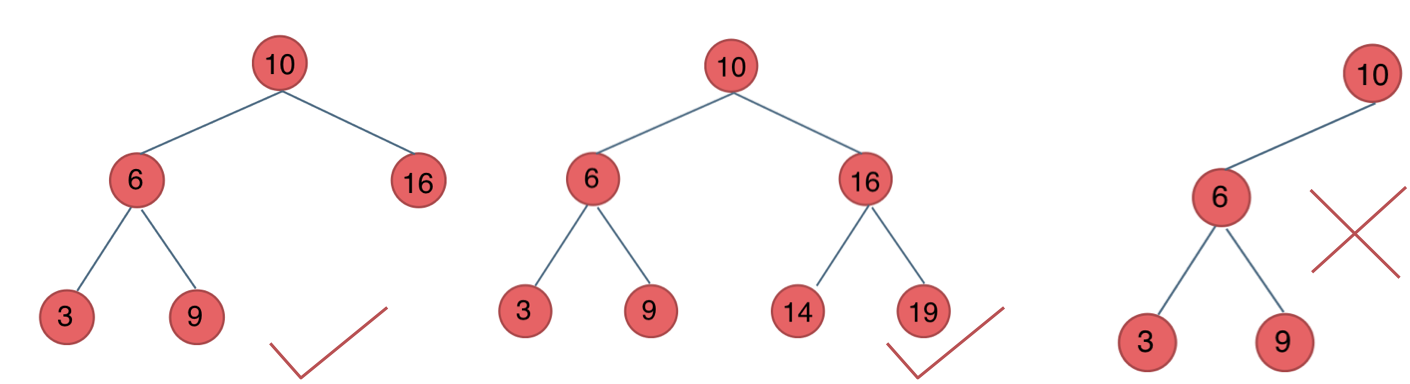
它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。
# 遍历方式
# 深度优先遍历
前序遍历(递归法,迭代法)
中左右中序遍历(递归法,迭代法)
左中右后序遍历(递归法,迭代法)
左右中
顺序针对的是 中 的位置
# 广度优先遍历
- 层次遍历(迭代法)
一层一层
# 递归遍历
- 确定递归函数的参数和返回值:传入树的节点;由于只是把值写进数组,所以没有返回值
- 确定终止条件:节点为空时终止
- 确定单层递归逻辑:添加对应节点值
# 前序遍历
type TreeNode struct { | |
Val int | |
Left *TreeNode | |
Right *TreeNode | |
} | |
//preorderTraversal 前序遍历 | |
// 中左右 | |
func preorderTraversal(root *TreeNode) []int { | |
var result []int | |
// 构造一个函数然后调用自己 | |
var traversal func(node *TreeNode) | |
traversal = func(node *TreeNode) { | |
if node == nil { | |
return | |
} | |
result = append(result, node.Val) | |
traversal(node.Left) | |
traversal(node.Right) | |
} | |
traversal(root) | |
return result | |
} |
# 中序遍历
type TreeNode struct { | |
Val int | |
Left *TreeNode | |
Right *TreeNode | |
} | |
//inorderTraversal 二叉树的中序遍历 | |
// 左中右 | |
func inorderTraversal(root *TreeNode) []int { | |
var result []int | |
var traversal func(node *TreeNode) | |
traversal = func(node *TreeNode) { | |
if node == nil { | |
return | |
} | |
traversal(node.Left) | |
result = append(result, node.Val) | |
traversal(node.Right) | |
} | |
traversal(root) | |
return result | |
} |
# 后序遍历
type TreeNode struct { | |
Val int | |
Left *TreeNode | |
Right *TreeNode | |
} | |
//postorderTraversal 二叉树的后序遍历 | |
// 后序遍历的流程是先遍历左子树,然后遍历右子树,最后访问根节点。 | |
// 这种遍历方式可以用于获取二叉树的后序遍历结果,常用于删除二叉树的操作。 | |
// 在遍历过程中,根节点的值总是在最后被访问。 | |
func postorderTraversal(root *TreeNode) []int { | |
var result []int | |
var traversal func(node *TreeNode) | |
traversal = func(node *TreeNode) { | |
if node == nil { | |
return | |
} | |
traversal(node.Left) | |
traversal(node.Right) | |
result = append(result, node.Val) | |
} | |
traversal(root) | |
return result | |
} |
# 迭代遍历
# 前序遍历
- 每个节点先推右孩子,再推左孩子
type TreeNode struct { | |
Val int | |
Left *TreeNode | |
Right *TreeNode | |
} | |
func preorderTraversal(root *TreeNode) []int { | |
var res []int | |
if root == nil { | |
return nil | |
} | |
st := list.New() | |
st.PushBack(root) | |
for st.Len() > 0 { | |
node := st.Remove(st.Back()).(*TreeNode) | |
res = append(res, node.Val) | |
if node.Right != nil { | |
st.PushBack(node.Right) | |
} | |
if node.Left != nil { | |
st.PushBack(node.Left) | |
} | |
} | |
return res | |
} |
# 中序遍历
- 如果
cur不为空,说明还有左子树未遍历
type TreeNode struct { | |
Val int | |
Left *TreeNode | |
Right *TreeNode | |
} | |
func inorderTraversal(root *TreeNode) []int { | |
var res []int | |
if root == nil { | |
return nil | |
} | |
st := list.New() | |
cur := root | |
for cur != nil || st.Len() > 0 { | |
if cur != nil { | |
st.PushBack(cur) | |
cur = cur.Left | |
} else { | |
cur = st.Remove(st.Back()).(*TreeNode) | |
res = append(res, cur.Val) | |
cur = cur.Right | |
} | |
} | |
return res | |
} |
# 后序遍历
- 先推左孩子,再推右孩子
左右中的结果恰好与中右左相反
type TreeNode struct { | |
Val int | |
Left *TreeNode | |
Right *TreeNode | |
} | |
func postorderTraversal(root *TreeNode) []int { | |
var res []int | |
if root == nil { | |
return nil | |
} | |
var st []*TreeNode | |
st = append(st, root) | |
for len(st) > 0 { | |
node := st[len(st)-1] | |
st = st[:len(st)-1] | |
res = append(res, node.Val) | |
if node.Left != nil { | |
st = append(st, node.Left) | |
} | |
if node.Right != nil { | |
st = append(st, node.Right) | |
} | |
} | |
reverse(res) | |
return res | |
} | |
func reverse(res []int) { | |
head := 0 | |
tail := len(res) - 1 | |
for head < tail { | |
res[head], res[tail] = res[tail], res[head] | |
head++ | |
tail-- | |
} | |
} |
# 层序遍历
type TreeNode struct { | |
Val int | |
Left *TreeNode | |
Right *TreeNode | |
} | |
func levelOrder(root *TreeNode) [][]int { | |
if root == nil { | |
return nil | |
} | |
var res [][]int | |
curLevel := []*TreeNode{root} | |
for len(curLevel) > 0 { | |
var nextLevel []*TreeNode | |
var vals []int | |
for _, node := range curLevel { | |
vals = append(vals, node.Val) // 收集当前的值 | |
// 收集下一层的节点 | |
if node.Left != nil { | |
nextLevel = append(nextLevel, node.Left) | |
} | |
if node.Right != nil { | |
nextLevel = append(nextLevel, node.Right) | |
} | |
} | |
res = append(res, vals) | |
curLevel = nextLevel | |
} | |
return res | |
} |
# 二叉树的最大深度
每个节点处的深度为孩子节点的最大深度 + 1
递归到空指针时表明上一级深度为 1(0+1)
type TreeNode struct { | |
Val int | |
Left *TreeNode | |
Right *TreeNode | |
} | |
func maxDepth(root *TreeNode) int { | |
// 终止条件 | |
if root == nil { | |
return 0 | |
} | |
left := maxDepth(root.Left) | |
right := maxDepth(root.Right) | |
maxDep := max(left, right) | |
return maxDep + 1 | |
} | |
func max(a, b int) int { | |
if a > b { | |
return a | |
} | |
return b | |
} |